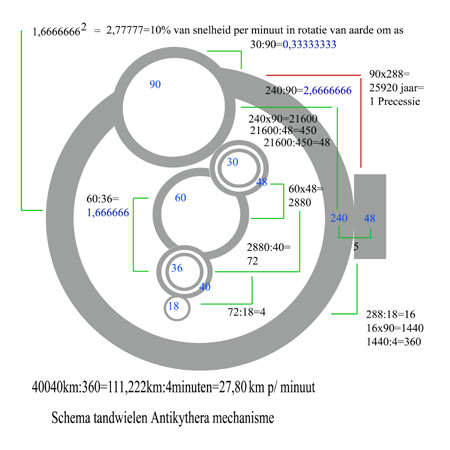
Het tandwielschema van een gedeelte van het mechanisme van Antikythera. De illustratie toont een klein gedeelte van de data die in het mechanisme verborgen zit; ‘tussen’ de tandwielen in hangt nog veel meer informatie. Die informatie kan eruit worden gehaald door de data van het oude apparaat te analyseren. Het is en blijft een uiterst vreemd geval, dat mechanisme van Antikythera; in het apparaat zit een energiefrequentie verborgen die de oplossing geeft voor de Priemgetallen reeks; 1,66666 of een tiende daarvan; 0,166666. Een trilling en zijn resonantie?

(Geschreven door Nellie Quist. Gepost op 6 maart 2010 om 20.26 uur.)

Illustratie;  schema van tandwielen in het Antikythera mechanisme

Deel je een Priemgetal door 6 (1 gedeeld door 0,166666 is 6) dan krijg je als basis van die trilling het nummer van dat getal in een van de reeksen. Wanneer je deze trilling loslaat op de priemgetallen reeks dan is die uitkomst op je calculator het Spronggetal van dat Priemgetal; zo is 7 gedeeld door 0,166666* is 42. Het getal 7 springt rond met een tussenpauze van 42 in zowel positieve als negatieve reeksen>> 7 plus 42 is 49 en dat is heel correct het volgende nummer in die reeks. (*0.166666 is 60 gedeeld door 360 (graden?))

De trilling met betrekking tot de getallen
Ook getallen schijnen te ontstaan door trillingen; roterende trillingen. Ik probeerde een oude truc uit de doos van de ontwerpers van het mechanisme; deel een getal door 6 en bekijk zijn frequentie:

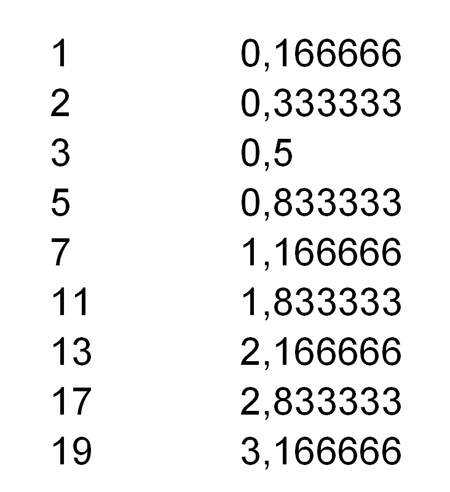Tabel 1; Leuke tabel, maar zien we nu een ritme verschijnen? Ja, zeker maar de tabel is niet geordend en in het ritme van de wel geordende getallen passen de getallen 2 en 3 niet; jammer maar helaas voor alle denkers op wiskundig gebied die verknocht waren aan de getallen 2 en 3 in de Priemlijn.

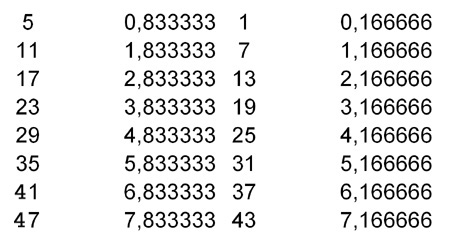
Tabel 2; De geordende tabel geeft een keurig overzicht van een oplopende frequentie; ieder volgend getal bestaat uit het vorige frequentie +1(x6).

 Wat mij uiteindelijk bracht op 4 getalslijnen die aan elkaar verwant zijn; mogelijk een D-Brane. Sommige samengestelde Priemgetallen gedeeld door 6 kunnen worden aangevuld met de frequentie van hun delers en vormen dan een geheel getal waardoor ze kunnen worden gedeeld! Zo geeft 25/4,16666+0,83333 = 25/5=5>5×5=25 en 35/5,83333+1,16666=7=5>7×5=35!

Maar bij andere nummers moet je juist de frequenties aftrekken tot hun delers;

49/8,16666-1,16666=7>49:7=7

77/12,83333-1,16666=11>77:11=7

(Let op; de frequenties moeten natuurlijk uitkomen op een oneven getal dat een element is van onze verzameling P-P-getallen, namelijk; X maal 6(+1) of X maal 6(-1) waarvoor geldt dat X is een element van N; de verzameling van de natuurlijke getallen!)

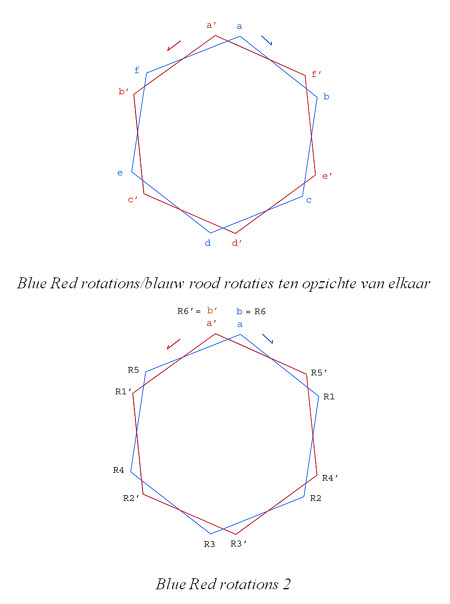
Illustratie 3; Twee simpel ogende regels bepalen de verschillende getallenrechten in een D-Braan: de Potentiële Priemgetal lijnstukken die zij vormen draaien ten opzichte van elkaar tegengesteld en bevatten alle Priemgetallen. Tussen de twee strengen zit een Point-Zero functie die niet gelijk is aan 0. Het punt bevindt zich op de locatie van 1 maar is niet helemaal gelijk aan 1 want het punt heeft, vreemd genoeg, ook de waarde -1! In het Point-Zero punt gaan kosmische krachten om waar wij nog helemaal niet het fijne van weten.

X maal 6 (+1) of X maal 6 (-1) is een goed getal; het is een element van onze verzameling

Wat opvalt, is dat de getallen met vaste regelmaat verschijnen en dat de Priemgetallen een voorkeur hebben voor het getal 6; ze zijn namelijk allemaal opgebouwd uit; X maal 6(+1) of X maal 6(-1), waarbij X is een element van N; de verzameling van de natuurlijke getallen.

(Bijvoorbeeld 7=1×6(+1) en 11 is weer 2×6(-1).) Maar wat zijn nou precies de spelregels van dit kosmische bordspel? Alle mogelijke priemgetallen bestaan uit een veelvoud van 6(+1) of

6(-1) en springen over het speelbord met sprongen van (X maal 6) hun basis waarde;

(7 bijvoorbeeld, verspringt graag met 6×7= 42 en maakt sprongetjes van bijvoorbeeld 7 naar 49 =7×7, 49+42=91=13×7, 91+42=133=19×7 enz.

(! 11×7=77 en 17×7=119 etc. zitten in de andere – en dus negatieve kant van de lijn!). Een soort damspelletje met dobbelstenen dus en wanneer je de achterkant raakt, dan krijg je een dam; Priem kwadraat!

Hocus Pocus met getallen? Nee!
Want waar kwam het getal 7 nu vandaan dan? Getal 7 kwam van 35 negatief = -35 (=-5×7). Het getal 42 huppelde door een Zero-functie ons positieve speelbord binnen. Het liet -35 achter en vormde 7 waarna het doorhuppelde naar (7+42=49) 49.

Bewijs? Ja; deel 7 door 6; =1,16666667 (en staat op de 1e plaats in deze +lijn). 49:6=8,16666666 (en staat op de 8^e plaats in deze positieve lijn) maar 35:6=5,833333 staat op de 5^e plaats in de negatieve lijn.

Hoe vinden we nu de priemgetallen? Onze zogenaamde ‘Priemgetallen’ zijn die getallen die net uit een nulpunt tevoorschijn kwamen en dus eigenlijk een stukje missen; 7 mist 35=42 compleet en 11 mist 55=66 compleet.

11:6=1,8333333>66:1,833333=36 (36=rotatie factor; ook 42 ( het spronggetal van 7) geeft natuurlijk 42:1,166666=36)

55:0,833333(x6=5)=66

De tafel van 11 op ons kosmische speelbord>>(….,-341,-275,-209,-143, -77,-11,55,121,187,253,319,385,… )etc. (Over 180 graden gespiegeld; verandert positief in negatief en negatief in positief.)

Verband met eiwitketens in het DNA?
In de nu ontstane 4 lijnstukken zitten ook nummers die niet zuiver priem zijn, maar ze zijn allemaal wel opgebouwd uit priemfactoren (Combinatie Priem); dat moet ook. Waarom? Omdat zonder deze nummers, je niet meer kunt zien hoe de lijnen verlopen en het nummerraster* voor de Priemberekeningen niet meer kloppend is te krijgen. Bedenk daarbij dat
eiwitketens in ons lichaam uiteen zouden vallen wanneer het afweersysteem in ons lichaam deze stukjes zou aanvallen en vernietigen. Alle nummers horen in de 4 lijnen; ze zijn immers opgebouwd uit Priemfactoren!

*(Nummerraster; In de geologie/mineraalkunde wordt ook gebruik gemaakt van zogenaamde kristalrasters; een netwerk van moleculen die bepaalde stoffen vormen. Door middel van een nummerraster kunnen we ook tafels van priemgetallen rasteren en in kaart brengen.)

Tabel 4; Nummerraster van twee lijnstukken; + en -+. Plus maal Plus blijft natuurlijk Plus. De hele getallen geven de getallen in de Potentiële Priemgetallen reeks (positief gedeelte). De getallen met 166666 achter de komma, geven de frequentie van die getallen.

Zowel de Priemreeks als de berekeningen voor planeetrotaties met het mechanisme hebben te maken met een 6 of 60-tallig stelsel; dat stelsel heeft alles te maken met 0,1666666 en 1,6666666. Het was misschien wel daarom dat de oude Soemeriërs een 60-tallig rekenstelsel (het sexagesimale stelsel) hadden en ook onze kloktijd ontwikkelde met als basis 60 seconden in 60 minuten = 1 uur. Dat rekent een heel stuk makkelijker wanneer je de banen van de planeten wilt berekenen met een cirkel van 360 graden in het rond.

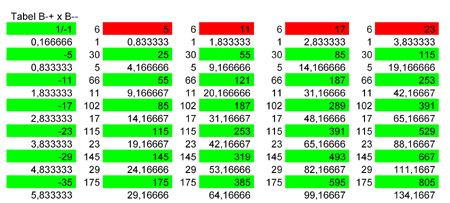
 Tabel 5; Nummerraster van twee andere lijnstukken; B-+ x B’–; van -0,83333 naar 4,166666 is het natuurlijk 5(x6=30×0,1666666). Aangezien de beide lijnen in feite negatief zijn; vormen ze samen een positief getal! (- maal – = +!)

Hoever lopen de lijnen door?
De lijnen roteren maar komen niet op hun beginpunt uit: planeten roteren maar komen na een jaar ook niet op hun exacte startpunt terug. Hun rotatiebaan verruimt na iedere ronde iets waardoor ze nooit op één van hun oude punten terug kunnen komen. De baan van de planeet draait verder en verder. De 4 Potentiële Priemlijnen lopen evenzo alsmaar verder en verder in de oneindigheid van de ruimtetijd, hoewel de echte “Priemgetallen” steeds verder uit elkaar komen te liggen.

(!)In een enkele lijn van deze Potentiële Priemgetallen zul je nooit twee nummers tegenkomen die positief/negatief aan elkaar gelijk zijn; bijvoorbeeld; -7 zit in een andere streng dan 7. Dit is conform het “Uitsluitingprincipe” van W. Pauli; hij zei dat deeltjes met de zelfde spin/draai nooit dezelfde ruimte of dimensie kunnen delen. (Tegengestelde spins kunnen dat misschien alleen ingeval er Speciale Relativiteitomstandigheden zijn?)

Kun je aan een getal zien van welke Priemlijn(en) het afkomstig is?
Ja; dat kun je zien aan de frequentie als je het getal deelt door bijvoorbeeld 3 of 6 (6 heeft mijn voorkeur).

77:6=12,83333333(77):1,16666666(=7)=11:6=1,8333333=11  en 77 is 11 x 7 (11 is 1^e P op A’ minus lijn maal 7 is 1^e P op A plus lijn)

49:6=8,16666666:1,16666666=7:6=1,166666=7×7 (is 1^e A’-lijn maal 1^e plaats op A-lijn)

221:6=36,8333333:2,1666666(=13)=17=2,833333 (en staat p de 2^e plaats:13 is de 2^e P op A-lijn,17 is de 2^e P de A’-lijn).

Maar pas op; we hebben vier lijnstukken, namelijk; twee dubbele lijnen met een positief gedeelte en een negatief gedeelte). (Kwantum fysica; Ingeval de beide strengen toch de zelfde ruimte delen moet er sprake zijn van een soort magnetisch veld of een ander soort membraan dat hen scheidt. Anders is het mogelijk dat de som van de beide deeltjes Nul wordt.)

In die 4 lijnstukken zitten bijvoorbeeld de getallen;
-7 (de lijn begint op -1)

7 (de lijn begint op +1)

-5 (de lijn begint op +1)

5 (de lijn begint op -1)

 

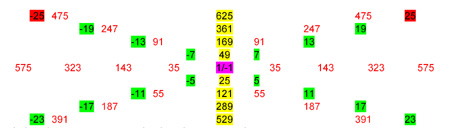
 Tabel 6; Groen is Priem, geel is kwadraat en rood is niet zuiver priem maar samengesteld of Combi-Priem, het nulpunt (paars) is in feite een zwart gat?Maar let op; dit punt is niet gelijk aan O! Nul is immers geen element van onze verzameling. 1:6=0,16666666 en dat is niet gelijk aan nul. Het Nulpunt (1/-1) van de beide strengen is dus een Nulpunt Functie; een soort Zwart Gat! Maar het punt is zeker niet gelijk aan nul!

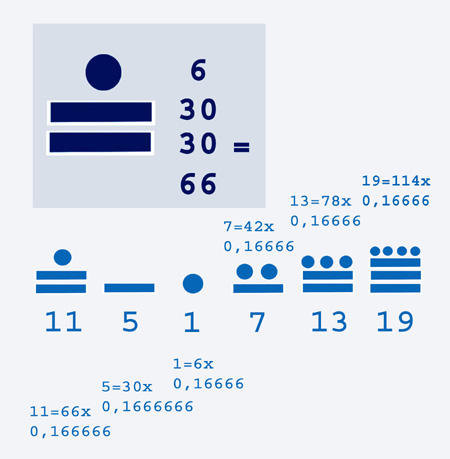
Zijn er nu aanwijzingen te vinden dat oude wetenschappers dit ook al wisten? Ja, die aanwijzingen zijn misschien te vinden. Een voorbeeld daarvan is het Maya telsysteem. Wanneer we ons baseren op de frequenties van 0,16666666(x6=1) en 0,8333333(x6=5) dan vinden we de volgende mogelijkheid;

Een ruitje is 0,16666666 maal 6 (5+1 voor de resonantie)=1 (een Maya stip voor het getal 1) en 6 maal 0,833333 = 4,999999=5 ; een plat balkje is een Maya 5. Point-Zero berekeningen;

6x6x6x6=1296>>3600:1296=2,7777777 en 111,222 km/boograad in 4 minuten : 2,7777 =40×6=1440 minuten=een omwenteling van de aarde in 24 uur om haar eigen as.

864***x5=4320:0,16666=25920=1 Precessie, 5184:1,2=4320:1,2=3600 en 1200×1,2 is 1440>>3600:1440=2,5 en 4320:1200=3,6 en 90:60=1,5. Al de gevonden getallen komen voor in de berekeningen rondom de tandwielen in het mechanisme van Antikythera. (***Het getal 864 of de helft ervan 432; We hebben het hier vermoedelijk over Hertz!)

Illustratie; het getal 7 springt rond met een tussenpauze van 42. Het volgende positieve nummer is dan 49. Het eerste negatieve nummer is -35 (-5×7). Zoals bekend is kenden de Maya’s ook al het getal Zero; een ovaal met twee schuin verticaal staande streepjes erdoor. Nemen we een Priemgetal en verlengen we deze maal 6 dan geeft dat voor het getal 7; 7-42= -35. 35+14=49= Priem kwadraat van 7. In het midden zien we het zwarte veld dat 35 + 7 =42 uitbeeldt. 35×1,2 (1,2 is de uitzettingsfactor voor trillingen) geeft ook 42. Dit getal van 6 maal de waarde van 7 is de Sprongfactor van het getal 7;
7+42 =49 en 49+42= 91(13×7) en in het negatieve geeft -35 – 42 = -77(=-11×7) etc. Let op; dit Maya teken betekende waarschijnlijk niet O/Nul/niets maar Point Zero! In deze Point-Zero-functie zitten diverse functies verborgen die te maken hebben met de kosmische energie-rotaties in dit Universum.

De krachten in Point-Zero
Point-Zero is het begin van zowel het negatieve lijnstuk als het positieve lijnstuk. De kosmische krachten die erin schuil gaan zijn zo exotisch dat wij die nog niet helemaal begrijpen. Toch doen we een speculatieve poging daartoe; Ingeval de negatieve lijn (die op -1 begint en via 5 naar 11 loopt) inderdaad bestaat uit hoofdzakelijk negatieve of donkere energie, dan lost dat in een klap een heleboel zaken op. We zochten naar de donkere energie of materie in dit universum maar al die tijd lag het voor onze neus en keken wij er overheen?

Kwantum fysici merkten onlangs al op dat delen van gewone materie, toch op de een of andere manier een negatieve uitstraling van energie hadden. Dat klopt dus blijkbaar helemaal.

Maar -1 is meteen de oorsprong van +1; om nu te stellen dat -1 maal -1 gewoon +1 wordt, is wel te simpel gesteld. In Point Zero bevinden zich -1 en +1 en buiten de cirkel bewegen diverse krachten die bestaan uit 5(+1) en 7(-1). Hoewel misschien simpel ogend, kunnen “in-en-om” dit punt enorme krachten roteren: de basis van die krachten zijn terug te voeren op een cyclus van 0,027777 (een duizendste van de rotatiesnelheid van de aarde om haar eigen as per minuut) x 3600 = 100 %  Die cyclus van 3600 is een van de basis cycli in het mechanisme van Antikythera ( de oude Babyloniers noemden dat getal een Saros; 3600 gedeeld door de kortste maancyclus van 26,66666 dagen=135 lunaties)! Die zelfde cyclus met betrekking tot de aardse rotaties, vinden we terug in de roterende getallen reeksen van de Potentiële Priemgetallen.

Illustratie; volgens de Maya telling zien de spronggetallen er dan natuurlijk zo uit.

Het vermoeden bestaat uit het volgende; de vorming van materie in dit universum wordt waarschijnlijk veroorzaakt door een trilling en de resonantie die daaruit voortkomt. De positieve kant van die trilling is een resultaat van een voortgaande trilling die komt uit het negatieve gedeelte. De reeks trillingen veroorzaakt specifieke resonanties die ervoor zorgen dat de materie in ons Universum wordt gevormd. Waar komen die trillingen vandaan?  Daar de trillingen eigenlijk oneindig zijn, is het antwoord daarop een erg moeilijke zaak die ver buiten onze horizon voor waarneming ligt.

Maar als we ons voorstellen dat we misschien alleen maar de positieve trillingen kunnen waarnemen, dan zou een object dat plotseling overgaat (versnelt of vertraagt) van de ene frequentie (0,1666666) op de andere (0,8333333) geheel plotseling verdwijnen uit ons blikveld, om misschien wel weer even later terug te komen in onze tijd, wanneer het weer terecht komt in het – voor ons zichtbare – trillingsveld. Een mogelijke verklaring voor het Ufo fenomeen en tevens ook een verklaring voor de vreemd in de tijd terug reizende deeltjes in het Kwantum fysica gebied?

Waar bestaan de priemgetallen dan mogelijk uit?

Het getal 7 bestaat dan mogelijk uit;
7-1,1666666=5,833333 >> 5,833333×1,2* =7

en komt van -35 met een sprong van 42 (6×7), waarna de tafel doorspringt naar 49.

-35 x 1,2 = -42 = spronggetal van 7.

*(De factor 1,2 met betrekking tot het getal 3600 (Saros) is dan
3600:0,83333= 4320:3600 =1,2 >>(0,833333×1,2=1) en 4320×1,2=5184=72×72 en 6×1,2=7,2) Factor 1,2; het getal is bekend als een uitzettingsfactor voor trillingen: bijvoorbeeld 0,833333(5×0,166666)x1,2=1 (0,999999 exact).

Het getal 1 bestaat in dan mogelijk uit; (een van de twee lijnen)

1-0,1666666=0,8333333×1,2=1

en komt van -5

-4,1666666×1,2= -5

en -1 komt van +5 (=de andere lijn).

5×1,2=6(=spronggetal van 1)

We komen dan tot een voorbeeldlijst van spronggetallen;
1=6>>-17,-11,-5,1,7,13 etc

-5=30>>-35,-5,25,55,85 etc.

-11=66>>-77,-11,55,121 etc.

-17=102>>

-23=138>>

-29=174>>

etc.

We zien dat tussen al deze getallen (hier een lijnstuk van een van de vier lijnstukken) een ruimte zit van 36(30:0,8333333=36)

36:0,1666666=216,008640*:30=7,200288012:0,833333=8,64:0,166666=51,84=7,2 x 7,2**

**7,2 = 6×1,2(1:0,833333=1,2!)

*8640:7,2=1200 (1200 is ook een belangrijke cyclus in het Mechanisme van Antikythera!)

 

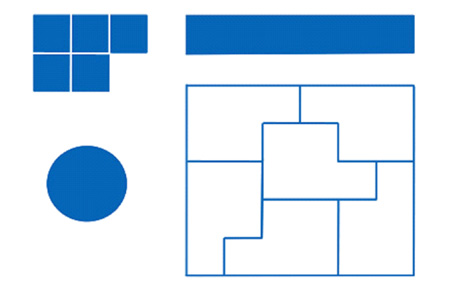
Basisraster van het verloop voor de Priemgetallen; boven de gele strook lopen twee lijnstukken vanuit het midden naar links en naar rechts. Alle getallen in de blauwe gedeelten zijn niet zuiver Priem maar Gecombineerd Priem. Alles wat dan over blijft is zuiver Priem!

Afgezet op een zesvlak (de Potentiële-Priem-Getallen die geproduceerd werden door de twee verschillende frequenties verlopen immers met de tafel van 6) betekent dit dat de nummers roteren in een tegengesteld draaiende maar gerelateerde puls (?) die gebaseerd is op de frequentie 6. We zagen al dat de eerste frequentie (na het centrale Nulpunt Point Zero 1/-1) = 1,166666667 =7 en dat het genoemde trillingsgetal het resultaat is van 1:6=0,16666666666×7…..etc.: een breuk met een irrationeel karakter want mogelijk loopt het getal door tot in het oneindige. (7 is dus 7×0,1666666×6=(42×0,16666666)=7)

Verder lezen? In deel 2 legt Nellie Quist het verband met het Mechanisme van Antikythera verder uit.

Nieuwe website linken over dit
onderwerp;

New Type Of Entanglement Allows ‘Teleportation in Time,’ Say Physicists;

17 januari 2011/kfc 01/17/2011
http://www.technologyreview.com/blog/arxiv/26270/
Extraction of timelike entanglement from the quantum vacuum;

14 januari 2011
http://arxiv.org/PS_cache/arxiv/pdf/1101/1101.2565v1.pdf